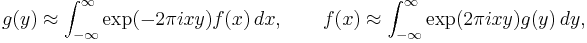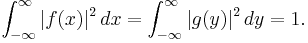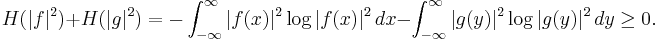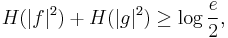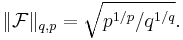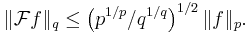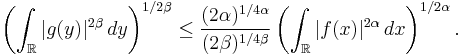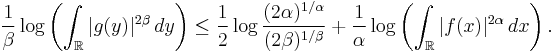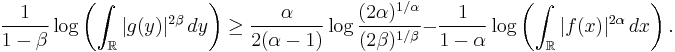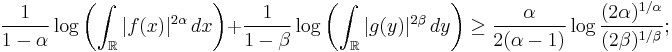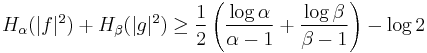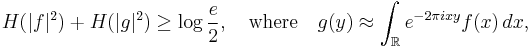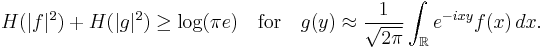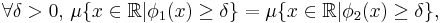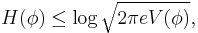Hirschman uncertainty

In quantum mechanics, information theory, and Fourier analysis, the Hirschman uncertainty is defined as the sum of the temporal and spectral Shannon entropies. It turns out that Heisenberg's uncertainty principle can be expressed as a lower bound on the sum of these entropies. This is stronger than the usual statement of the uncertainty principle in terms of the product of standard deviations.

In 1957,^[1] Hirschman considered a function f and its Fourier transform g such that

$g(y) \approx \int_{-\infty}^\infty \exp (-2\pi ixy) f(x)\, dx,\qquad f(x) \approx \int_{-\infty}^\infty \exp (2\pi ixy) g(y)\, dy,$

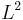where the " $\approx$ " indicates convergence in $L^2$ , and normalized so that (by Plancherel's theorem)

$\int_{-\infty}^\infty |f(x)|^2\, dx = \int_{-\infty}^\infty |g(y)|^2 \,dy = 1.$

He showed that for any such functions the sum of the Shannon entropies is non-negative:

$H(|f|^2) %2B H(|g|^2) = - \int_{-\infty}^\infty |f(x)|^2 \log |f(x)|^2\, dx - \int_{-\infty}^\infty |g(y)|^2 \log |g(y)|^2 \,dy \ge 0.$

A tighter bound,

$H(|f|^2) %2B H(|g|^2) \ge \log \frac e 2,$

was conjectured by Hirschman^[1] and Everett^[2] and proven in 1975 by W. Beckner.^[3]. The equality holds in the case of Gaussian distributions^[4],

1 Sketch of proof
2 Entropy versus variance
3 See also
4 References
5 Further reading

Sketch of proof

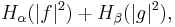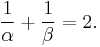The proof of this tight inequality depends on the so-called (q, p)-norm of the Fourier transformation. (Establishing this norm is the most difficult part of the proof.) From this norm we are able to establish a lower bound on the sum of the (differential) Rényi entropies $H_\alpha(|f|^2) %2B H_\beta(|g|^2),\,$ where $\frac 1\alpha %2B\frac 1\beta=2.$ For simplicity we shall consider this inequality only in one dimension; the extension to multiple dimensions is not difficult and can be found in the literature cited.

Babenko–Beckner inequality

The (q, p)-norm of the Fourier transform is defined to be^[5]

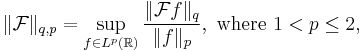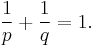
$\|\mathcal F\|_{q,p} = \sup_{f\in L^p(\mathbb R)} \frac{\|\mathcal Ff\|_q}{\|f\|_p},\text{ where }1 < p \le 2,$ and $\frac 1 p %2B \frac 1 q = 1.$

In 1961, Babenko^[6] found this norm for even integer values of q. Finally, in 1975, using Hermite functions as eigenfunctions of the Fourier transform, Beckner^[3] proved that the value of this norm (in one dimension) for all 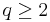$q \ge 2$ is

$\|\mathcal F\|_{q,p} = \sqrt{p^{1/p}/q^{1/q}}.$

Thus we have the Babenko–Beckner inequality that

$\|\mathcal Ff\|_q \le \left(p^{1/p}/q^{1/q}\right)^{1/2} \|f\|_p.$

Rényi entropy inequality

From this inequality, an expression of the uncertainty principal in terms of the Rényi entropy can be derived.^[5]^[7]

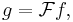
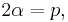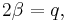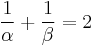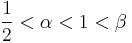Letting $g=\mathcal Ff,$ $2\alpha = p,$ and $2\beta=q,$ so that $\frac 1\alpha%2B\frac 1\beta=2$ and $\frac 1 2 < \alpha < 1 < \beta$ we have

$\left(\int_{\mathbb R} |g(y)|^{2\beta}\,dy\right)^{1/2\beta} \le \frac{(2\alpha)^{1/4\alpha}}{(2\beta)^{1/4\beta}} \left(\int_{\mathbb R} |f(x)|^{2\alpha}\,dx\right)^{1/2\alpha}.$

Squaring both sides and taking the logarithm, we get:

$\frac 1\beta \log\left(\int_{\mathbb R} |g(y)|^{2\beta}\,dy\right) \le \frac 1 2 \log\frac{(2\alpha)^{1/\alpha}}{(2\beta)^{1/\beta}} %2B \frac 1\alpha \log \left(\int_{\mathbb R} |f(x)|^{2\alpha}\,dx\right).$

Multiplying both sides by 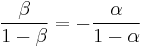$\frac{\beta}{1-\beta}=-\frac{\alpha}{1-\alpha}$ reverses the sense of the inequality:

$\frac {1}{1-\beta} \log\left(\int_{\mathbb R} |g(y)|^{2\beta}\,dy\right) \ge \frac\alpha{2(\alpha-1)}\log\frac{(2\alpha)^{1/\alpha}}{(2\beta)^{1/\beta}} - \frac{1}{1-\alpha} \log \left(\int_{\mathbb R} |f(x)|^{2\alpha}\,dx\right).$

Rearranging terms, we finally get an inequality in terms of the sum of the Rényi entropies:

$\frac{1}{1-\alpha} \log \left(\int_{\mathbb R} |f(x)|^{2\alpha}\,dx\right) %2B \frac {1}{1-\beta} \log\left(\int_{\mathbb R} |g(y)|^{2\beta}\,dy\right) \ge \frac\alpha{2(\alpha-1)}\log\frac{(2\alpha)^{1/\alpha}}{(2\beta)^{1/\beta}};$

$H_\alpha(|f|^2) %2B H_\beta(|g|^2) \ge \frac 1 2 \left(\frac{\log\alpha}{\alpha-1}%2B\frac{\log\beta}{\beta-1}\right) - \log 2$

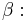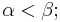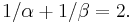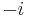Note that this inequality is symmetric with respect to $\alpha$ and $\beta:$ We no longer have to assume that $\alpha<\beta;$ only that they are positive and not both one, and that $1/\alpha%2B1/\beta=2.$ To see this symmetry, simply exchange the rôles of $i$ and $-i$ in the Fourier transform.

Shannon entropy inequality

Taking the limit of this last inequality as 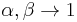$\alpha,\beta\rightarrow 1$ yields the Shannon entropy inequality

$H(|f|^2) %2B H(|g|^2) \ge \log\frac e 2,\quad\textrm{where}\quad g(y) \approx \int_{\mathbb R} e^{-2\pi ixy}f(x)\,dx,$

valid for any base of logarithm as long as we choose an appropriate unit of information, bit, nat, etc. The constant will be different, though, for a different normalization of the Fourier transform, (such as is usually used in physics,) i.e.

$H(|f|^2) %2B H(|g|^2) \ge \log(\pi e)\quad\textrm{for}\quad g(y) \approx \frac 1{\sqrt{2\pi}}\int_{\mathbb R} e^{-ixy}f(x)\,dx.$

In this case the dilation of the Fourier transform by a factor of 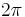$2\pi$ simply adds 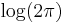$\log (2\pi)$ to its entropy.

Entropy versus variance

The Gaussian or normal probability distribution plays an important role in the relationship between variance and entropy: it is a problem of the calculus of variations to show that this distribution maximizes entropy for a given variance, and at the same time minimizes the variance for a given entropy. Moreover the Fourier transform of a Gaussian probability amplitude function is also Gaussian—and the absolute squares of both of these are Gaussian, too. This suggests—and it is in fact quite true—that the entropic statement of the uncertainty principle is stronger than its traditional statement in terms of the variance or standard deviation.

Hirschman^[1] explained that entropy—his version of entropy was the negative of Shannon's—is a "measure of the concentration of [a probability distribution] in a set of small measure." Thus a low or large negative Shannon entropy means that a considerable mass of the probability distribution is confined to a set of small measure. Note that this set of small measure need not be contiguous; a probability distribution can have several concentrations of mass in intervals of small measure, and the entropy may still be low no matter how widely scattered those intervals are.

This is not the case with the variance: variance measures the concentration of mass about the mean of the distribution, and a low variance means that a considerable mass of the probability distribution is concentrated in a contiguous interval of small measure.

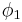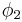To make this distinction more formal, we say that two probability density functions $\phi_1$ and $\phi_2$ are equimeasurable if:

$\forall \delta > 0,\,\mu\{x\in\mathbb R|\phi_1(x)\ge\delta\} = \mu\{x\in\mathbb R|\phi_2(x)\ge\delta\},$

where $\mu$ is the Lebesgue measure. Any two equimeasurable probability density functions have the same Shannon entropy, and in fact the same Rényi entropy of any order. The same is not true of variance, however. Any probability density function has a radially decreasing equimeasurable "rearrangement" whose variance is less (up to translation) than any other rearrangement of the function; and there exist rearrangements of arbitrarily high variance, (all having the same entropy.)

In fact, for any probability density function $\phi$ on the real line,

$H(\phi) \le \log \sqrt {2\pi eV(\phi)},$

where H is the Shannon entropy and V is the variance, an inequality that is saturated only in the case of a normal distribution.

References

^ ^a ^b ^c I.I. Hirschman, Jr., A note on entropy. American Journal of Mathematics (1957) pp. 152–156
^ Hugh Everett, III. The Many-Worlds Interpretation of Quantum Mechanics: the theory of the universal wave function. Everett's Dissertation
^ ^a ^b W. Beckner, Inequalities in Fourier analysis. Annals of Mathematics, Vol. 102, No. 6 (1975) pp. 159–182.
^ Ozaydin, Murad; Przebinda, Tomasz (2004). "An Entropy-based Uncertainty Principle for a Locally Compact Abelian Group". Journal of Functional Analysis (Elsevier Inc.) 215 (1): 241–252. http://redwood.berkeley.edu/w/images/9/95/2002-26.pdf. Retrieved 2011-06-23.
^ ^a ^b Iwo Bialynicki-Birula. Formulation of the uncertainty relations in terms of the Renyi entropies. arXiv:quant-ph/0608116v2
^ K.I. Babenko. An ineqality in the theory of Fourier analysis. Izv. Akad. Nauk SSSR, Ser. Mat. 25 (1961) pp. 531–542 English transl., Amer. Math. Soc. Transl. (2) 44, pp. 115-128
^ H.P. Heinig and M. Smith, Extensions of the Heisenberg–Weil inequality. Internat. J. Math. & Math. Sci., Vol. 9, No. 1 (1986) pp. 185–192. [1]